ISO/IEC 10918-1 : 1993(E)
Figure G.5 [99] = 7 cm = 273 %
TISO1620-93/d100
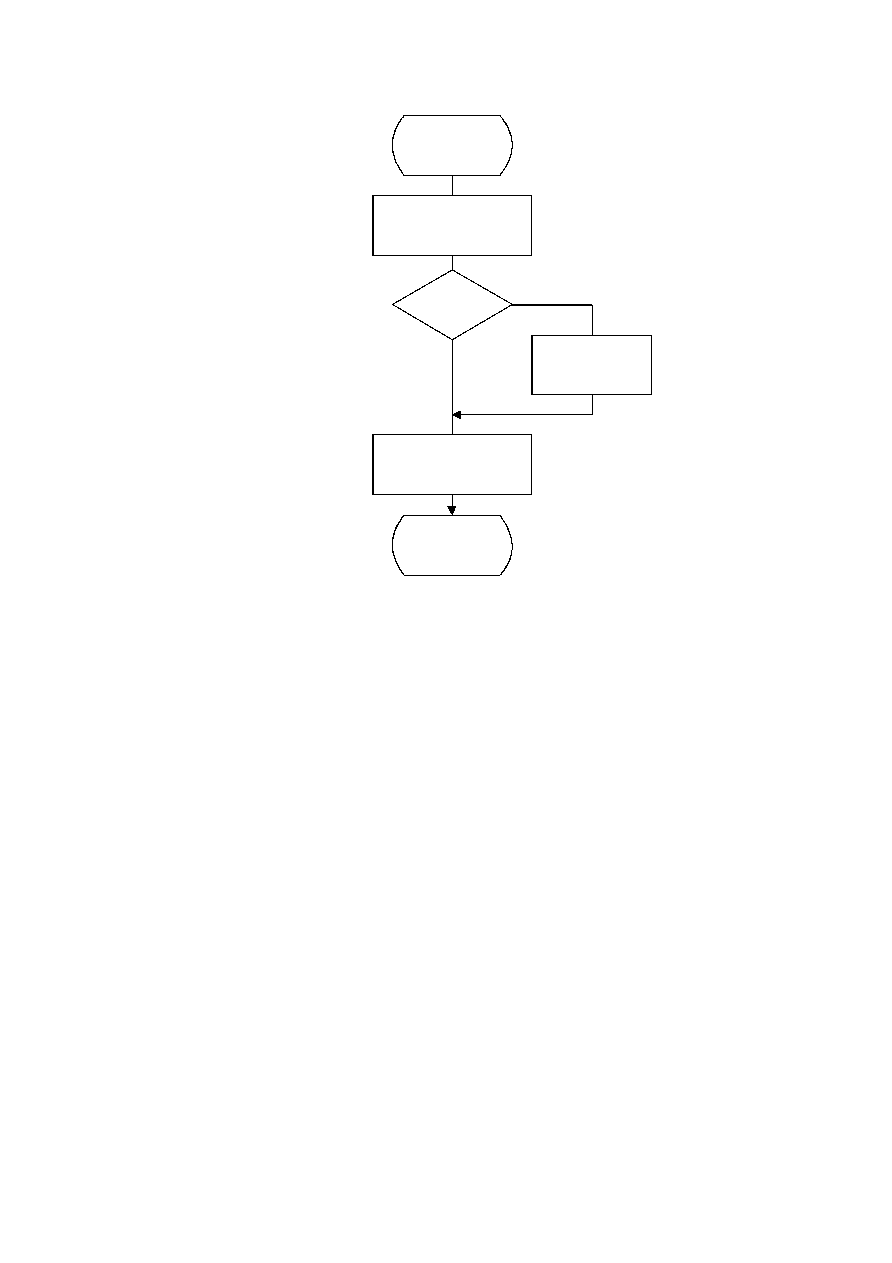
Encode_R_ZZ(K)
SSSS = CSIZE(ZZ(K))
I = (16 × R) + SSSS
Append EHUFSI(I)
bits of EHUFCO(I)
ZZ(K) < 0
?
Yes
No
ZZ(K) = ZZ(K) 1
Append SSSS low order
bits of ZZ(K)
R = 0
Done
Figure G.6 Encoding of the zero run and non-zero coefficient
Figure G.6 [D100] = 12.5 cm = 489 %
G.1.2.3 Coding model for subsequent scans of successive approximation
The Huffman coding structure of the subsequent scans of successive approximation for a given component is similar to the
coding structure of the first scan of that component.
The structure of the AC code table is identical to the structure described in G.1.2.2. Each non-zero point transformed
coefficient that has a zero history (i.e. that has a value
±
1, and therefore has not been coded in a previous scan) is defined
by a composite 8-bit run length-magnitude value of the form:
RRRRSSSS
The four most significant bits, RRRR, give the number of zero coefficients that are between the current coefficient and the
previously coded coefficient (or the start of band). Coefficients with non-zero history (a non-zero value coded in a
previous scan) are skipped over when counting the zero coefficients. The four least significant bits, SSSS, provide the
magnitude category of the non-zero coefficient; for a given component the value of SSSS can only be one.
The run length-magnitude composite value is Huffman coded and each Huffman code is followed by additional bits:
a)
One bit codes the sign of the newly non-zero coefficient. A 0-bit codes a negative sign; a 1-bit codes a
positive sign.
b)
For each coefficient with a non-zero history, one bit is used to code the correction. A 0-bit means no
correction and a 1-bit means that one shall be added to the (scaled) decoded magnitude of the coefficient.
CCITT Rec. T.81 (1992 E)
125
